引言
推荐系统
问题表述
首先来看看如何表达一个推荐系统的问题,假设有五个电影和四个用户,四个用户分别对五个电影进行打分:
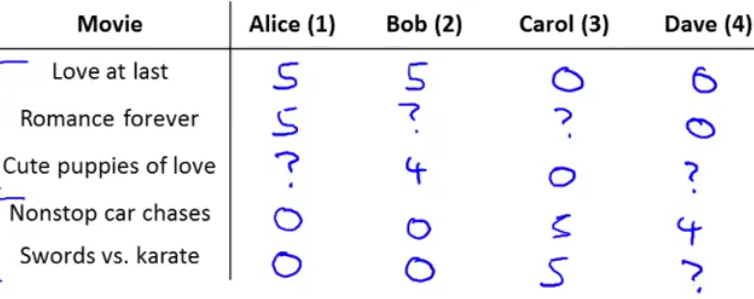
图中问号表示没有打分。然后定义一些变量:

从上到下分别是:
- 总共有几位用户
- 总共有几部电影
- 第j个用户是否给第i个电影打过分,如果打过就等于1
- 第j个用户给第i个电影打分的值
我们想做的事情就是,根据用户的打分,来填满用户没有打分的项,然后给他们推荐相关的信息。
基于内容的推荐
还是刚刚的看电影的例子,每个电影有两个特征量,一个是浪漫指数,一个是动作指数:
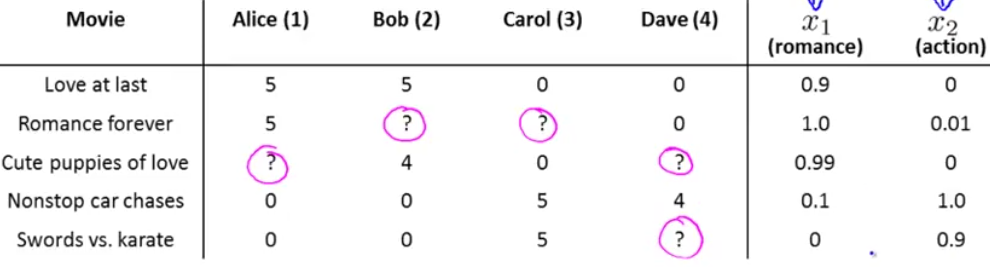
然后对于每一个用户,都看做一个线性回归问题,用已打分的来预测未打分的:
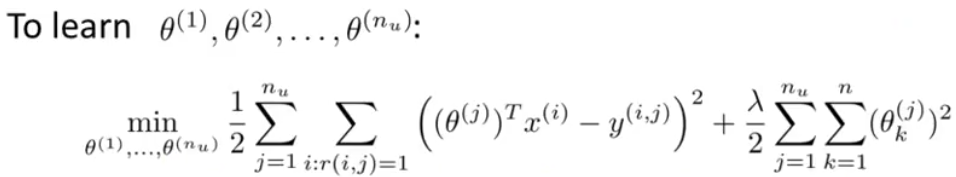
看起来很像最小二乘法拟合。把所有的放在一起就有如下全局目标函数:
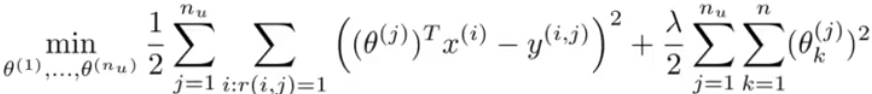
以及梯度函数:
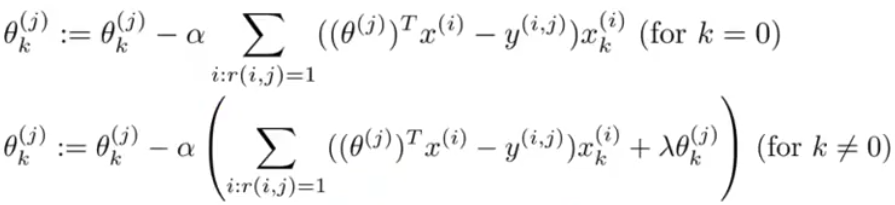
这种方法从本质上来说就是一种线性回归,但是你需要区分不同电影之间的特征。
协同过滤(Collaborative Filtering)
这个算法有个特点,就是能自主学习要使用的特征。
那么现在反过来假设,如果我们知道每个用户都喜欢哪一类电影,然后根据用户的喜好,来评估每一个电影的浪漫指数或者动作指数:

然后将两个算法拼在一起,先估计一组θ,然后计算x,用计算出来的x再来计算θ,循环往复,无穷尽也,最后两组值都会收敛到一个较好的结果。
这是一个最基本的想法,但是这样循环的算并不是很高效,而现在有更高效的方法同时算出两组值。
既然两个都需要优化,干脆就放在一个目标函数里面,一起优化不就好了?
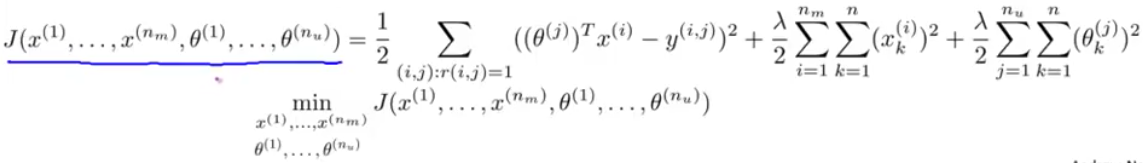
将将将将!!!终极目标函数诞生!
Tips: 这个里面的两组值,都没有x0=1这个变量。
那么梳理一下协同过滤算法的整个流程:
- 先随机初始化一组
x和一组θ。 - 使用梯度下降法。
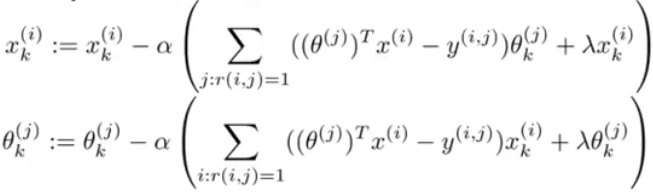
- 用学习到的值,预测用户对一个电影的打分。
向量化的话,如下图:

左边是打分,右边是对应的两个参数形成的预测打分。
均值归一化,会让你的算法表现更好哟~~~