从零开始搭建可灵活调整的神经网络

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

引言

从零开始搭建一种可灵活调整每层神经元数量、激活函数以及损失函数等参数的神经网络（框架）。

目标

本文的目标在于设计一种，可以用于拟合，也可以用于分类的神经网络。该神经网络可以灵活地调整每一层的神经元数量和各种参数。

本文对于神经网络的基本原理不会详细讲解，只会在适当的地方点一下，如有想学习基础原理的，请另寻他处。

设计思路

设计这种有点像小框架的东西，很需要思路。现有的思路有两种，一种是类似于Keras的，一种是类似于Tensorflow的。

我选了类似于Keras的，将神经网络作为一个实例，往实例里面添加层，在每一层里面设置相应的参数。然后往实例里面加入数据进行训练，就完成了一个模型。

整体架构

整体设计思路采用面向对象的方法，所以首先得有一个神经网络类，还需要一个神经层类。每个类有相应的方法。

神经网络类

神经网络类里面的方法包括如下这些：

  1. 构造函数。存放一些全局变量。
  2. 神经层添加函数。用于给神经网络添加神经层。
  3. 训练函数。控制训练流程。
  4. 前向传播函数。计算前向传播。
  5. 反向传播函数。计算反向传播。
  6. 预测函数。用于预测新的数据。
  7. 保存模型。
  8. 加载模型。

神经层类

神经层类的方法包括这些：

  1. 构造函数。
  2. 前向计算。
  3. 计算误差。
  4. 计算神经元梯度。
  5. 更新权值。
  6. 计算激活函数梯度。

通用函数

这里面还包括一些通用函数：

  1. sigmoid函数。
  2. sigmoid梯度函数。
  3. relu函数。
  4. relu梯度函数。
  5. softmax函数。
  6. softmax与交叉熵函数。
  7. softmax与误差函数。

通用函数

万事开头难，那我们就从简单的开始。

sigmoid函数及其梯度函数

1
2
3
4
5
6
def sigmoid(Z):
    return 1.0 / (1.0 + np.exp(-Z))


def sigmoid_gradient(Z):
    return sigmoid(Z) * (1.0 - sigmoid(Z))

relu函数及其梯度函数

1
2
3
4
5
6
7
8
9
def relu(Z):
    return np.maximum(0.0, Z)


def relu_gradient(Z):
    temp = np.array(Z, copy=True)
    temp[temp <= 0] = 0.0
    temp[temp > 0] = 1.0
    return temp

softmax函数及其反向传播相关函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def softmax(z):
    max_row = np.max(z, axis=-1, keepdims=True)  # 每一个样本的所有分数中的最大值
    tmp = z - max_row
    return np.exp(tmp) / np.sum(np.exp(tmp), axis=-1, keepdims=True)


def softmax_cross_entropy(logits, y):
    n = logits.shape[0]
    a = softmax(logits)
    scores = a[range(n), y]
    # scores = a[range(n), np.argmax(y, axis=1)]
    loss = -np.sum(np.log(scores)) / n
    return a, loss


def derivation_softmax_cross_entropy(logits, y):
    n = logits.shape[0]
    a = softmax(logits)
    a[range(n), y] -= 1
    # a[range(n), np.argmax(y, axis=1)] -= 1
    return a

这里尤其要说明一下这个softmax。

softmax可以作为中间层的激活函数（不推荐），也可以搭配交叉熵最为最后的激活函数进行多分类（强烈推荐）。但是用于分类的时候就有一点迷惑。

为什么要写softmax和softmax与交叉熵两个函数，而没有单独写交叉熵损失函数呢。（因为不好写XD！）其实是没必要写，因为反向传播的时候不单独算交叉熵的误差和梯度（这个确实是因为不好算），而是和softmax一起算，跳过了中间的步骤。公式推导可以看这里。

那又为啥要单独写一个softmax函数呢。因为前向传播分为两种(此处参考了这篇文章)：

  1. 推理预测时的前向传播。因为此时不需要计算loss，也不需要反向传播，就不需要用到softmax, 只用logits就可以做出预测，可以减少计算量（所以用softmax概率化后的得分也是可以的）。
  2. 训练时的前向传播。此时需要记录中间变量z和a,用于反向传播，所以需要进行softmax计算。

神经层

构造函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Layer:
    def __init__(self, layers_dims, activation='relu'):
        """
        构造函数
        :param layers_dims: (input_size, output_size) 权值矩阵的大小（上一层的神经元个数，本层的神经元个数）
        :param activation:  激活函数
        """
        self.W = 2.0 * np.random.random(layers_dims) - 1.0
        self.b = 0.0
        self.act = activation
        self.W_gradient = 1.0e-10
        self.b_gradient = 1.0e-10
        self.err = np.array([])
        self.gradiant = np.array([])
        self._input = np.array([])
        self._output = np.array([])

前向计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def _forward(self, X, Y):
    """
    神经层的前向计算
    :param X: 上一层的输出
    :param Y: 样本的标签，用于最后一层的计算。
    :return: 
    """
    self._input = np.dot(X, self.W) + self.b
    loss = 0
    if self.act == 'relu':
        self._output = relu(self._input)
        loss = self._output
    elif self.act == 'sigmoid':
        self._output = sigmoid(self._input)
        loss = self._output
    elif self.act == 'softmax':
        a, loss = softmax_cross_entropy(self._input, Y)
        self._output = a
    elif self.act == 'linear':
        self._output = self._input
        loss = self._output
    return self._output, loss

计算本层误差

1
2
3
4
5
6
7
8
9
10
11
12
def count_err(self, front_err, Y):
    """
    计算本层的误差
    :param front_err: 后一层的误差
    :param Y: 样本的标签，用于最后一层的计算。
    :return:
    """
    if self.act == 'softmax':
        self.err = derivation_softmax_cross_entropy(self._input, Y)
    else:
        self.err = front_err * self.act_gradient(self._input)
    return self.err

依据的公式为如下两个，第一个是最后一层的误差：

中间层的误差：

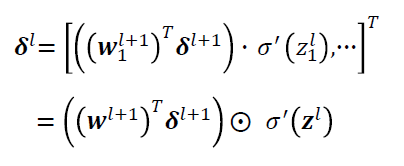
解释一下上面的式子。记每一层输入到神经元的输入记为z，也就是w*x，其中的x为上一层的输出，w为这一层的权值。

先看最后一层，最后一层的误差等于损失函数的梯度乘以这一层激活函数的梯度。

然后对于中间层，这一层的误差等于本层激活函数的梯度乘以（后一层的w乘以后一层的误差）。

如果将损失函数也看做一个神经层，最后一层和损失函数之间的权值w=1，那么损失函数的梯度就可以看做是最后一层的后一层的误差。就可以将上面的汇总成一个。

计算本层权值的梯度

1
2
3
4
5
6
7
def count_gradient(self, al_1):
    """
    
    :param al_1: 前一层的a
    :return:
    """
    self.gradiant = np.dot(al_1.T, self.err)

计算权值梯度就是用前一层的a乘以自己这一层的误差。a表示一层神经元经过激活函数后的输出。

更新权值

1
2
3
4
5
6
7
8
9
def update_parameters(self, rate, n):
    """

    :param rate: 学习率
    :param n: batch_size
    :return:
    """
    self.W = self.W - rate * self.gradiant / n
    self.b = self.b - rate * np.sum(self.err) / n

本层激活函数的梯度

1
2
3
4
5
6
7
8
9
10
11
12
def act_gradient(self, Z):
    """

    :param Z: 本层的Z
    :return:
    """
    if self.act == 'relu':
        return relu_gradient(Z)
    elif self.act == 'sigmoid':
        return sigmoid_gradient(Z)
    elif self.act == 'linear':
        return 1

小结

将不同的激活函数、不同的层都集中到一个方法里面，是为了更好的实现面向对象编程，实现方法复用。

神经网络

构造函数

1
2
3
4
class NeuralNetwork:

    def __init__(self):
        self.NN = []

用于存放神经层的。

添加神经层

1
2
3
4
5
6
7
8
def add_layer(self, layers_dims, activation='relu'):
    """
    
    :param layers_dims: (input_size, output_size) 权值矩阵的大小（上一层的神经元个数，本层的神经元个数）
    :param activation: 激活函数
    :return: 
    """
    self.NN.append(Layer(layers_dims, activation))

前向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def forward(self, X, Y, mission):
    """
    
    :param X: input
    :param Y: output
    :param mission: 分类还是拟合 regression | classification
    :return: 
    """
    temp = X
    loss = 0.0
    for nn in self.NN:
        temp, loss = nn._forward(temp, Y)
    if mission == 'regression':
        temp = self.NN[-1]._input
    return temp, loss

反向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def backward(self, out, x, y, rate, mission):
    """
    反向传播
    :param out: 拟合时的输出
    :param x: 样本特征
    :param y: 样本标签
    :param rate: 学习率
    :param mission: 分类还是拟合 regression | classification
    :return: 
    """
    self.NN.reverse()
    _err = 0.0
    if mission == 'regression':
        _err = 2 * (out - y)
    for i in self.NN:
        _err = i.count_err(_err, y)
        _err = np.dot(_err, i.W.T)
    if len(self.NN) > 1:
        for i in list(range(len(self.NN)))[0:-1]:
            self.NN[i].count_gradient(self.NN[i + 1]._output)
    self.NN[-1].count_gradient(x)
    self.NN.reverse()
    for i in self.NN:
        i.update_parameters(rate, y.shape[0])

在这里要特别注意，因为反向传播是从后往前算，所以我在最开始将神经层逆序了，在最后又逆序回来了。然后拟合的损失函数用的平方损失函数，就没有单独拿出来了，有兴趣的同学可以自己改，改成不同的损失函数。

训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def train(self, x, y, mission, epochs=1000, batch_size=50, learning_rate=0.01, data_rate=0.6, target=None, print_cost=False):
    j = 0
    x_train, y_train, x_val, y_val = load_data(x, y, data_rate)
    cost_his = []
    while j < epochs:
        # 训练
        x_batches, y_batches = load_batches(x_train, y_train, batch_size)
        for i, (temp_x, temp_y) in enumerate(zip(x_batches, y_batches)):
            out, cost = self.forward(temp_x, temp_y, mission)
            self.backward(out, temp_x, temp_y, learning_rate, mission)

        # 验证
        j += 1
        if print_cost and j % 10 == 0:
            x_batches, y_batches = load_batches(x_val, y_val, batch_size)
            costs = 0
            acc = 0.0
            n = x_val.shape[0]
            for i, (temp_x, temp_y) in enumerate(zip(x_batches, y_batches)):
                out, cost = self.forward(temp_x, temp_y, mission)
                if mission == 'regression':
                    costs += np.sum((temp_y - out) ** 2)
                elif mission == 'classification':
                    logits = self.NN[-1]._input
                    correct = np.sum(np.argmax(logits, axis=-1) == temp_y)
                    acc += correct
                    costs += cost
            costs /= n
            cost_his.append(costs)
            acc /= n
            if mission == 'classification':
                print("epochs %i cost value: %f, acc value: %f" % (j, costs, acc))
            elif mission == 'regression':
                print("epochs %i cost value: %f" % (j, costs))

            if target != None:
                if mission == 'regression':
                    if float(costs) < target:
                        break
                    elif j == epochs:
                        j = 0
                        learning_rate *= 0.95
                elif mission == 'classification':
                    if float(acc) > target:
                        break
                    elif j == epochs:
                        j = 0
                        learning_rate *= 0.95

训练的话就没什么特别需要注意的了，都是老生常谈。只是里面的load_data和load_batch两个函数我没有在这里给出，详情可以看我的github，在最后给出链接。

预测

1
2
3
4
5
6
7
8
9
10
11
12
def predict(self, x, y, mission):
    if mission == 'regression':
        temp = x
        for nn in self.NN:
            temp, loss = nn._forward(temp, y)
        return temp
    elif mission == 'classification':
        temp = x
        for nn in self.NN:
            temp, loss = nn._forward(temp, y)
        logits = self.NN[-1]._input
        return np.argmax(logits, axis=-1) + 1

预测也没什么好说，就是前向传播，然后分了回归和分类两个任务。

保存和加载

1
2
3
4
5
6
7
8
def save_model(self, name):
    with open(name, 'wb') as f:
        pickle.dump(self, f)

def load_model(self, f_d):
    with open(f_d, 'rb') as f:
        a = pickle.load(f)
        self.NN = a.NN

用的是Python自带的pickle库，还是挺好使的。

总结

中间很多都是一笔带过，其实只是涉及实现的话，我觉得难点在于以下几点：

  1. 将分类和回归的正反传播结合起来。
  2. 弄懂神经网络最后一层和损失函数之间该怎么反向传播，特别是分类的时候。Tips:我觉得这里可以将损失函数也理解成一层，但是和最后一层的输出是直连，中间的权值为1。
  3. 弄懂softmax和交叉熵怎么一起算反向传播。

后记

更详细更全面的代码，可以看我的github。欢迎Star~