引言
高大上的无监督学习正在路上,从这篇开始就是无监督学习了,我觉得无监督学习和有监督学习的结合,才是机器学习的未来,特别是深度学习。
无监督学习
无监督学习就是给定数据集,没有给定对应的标签,让机器自己学习数据之间的结构和关系。
K-Means聚类法
这个K-Means聚类算法是现在用的最广的一种,我之前也用过,却没有了解过其中的原理。
工作流程示意
首先假设这里有两簇数据,而且没有给定标签:
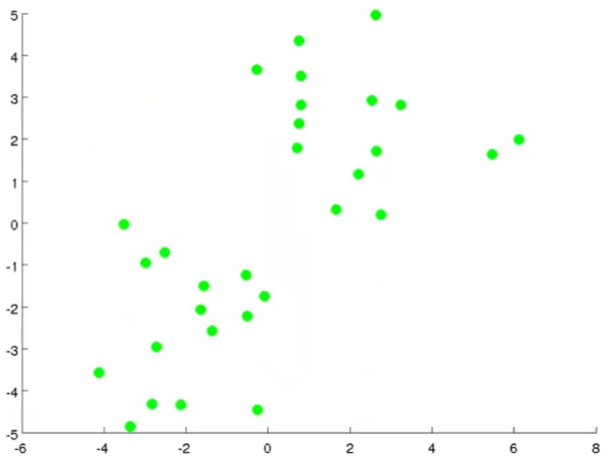
1.首先假设我们想将数据分为两类。所以先取两个点,称作聚类中心点:
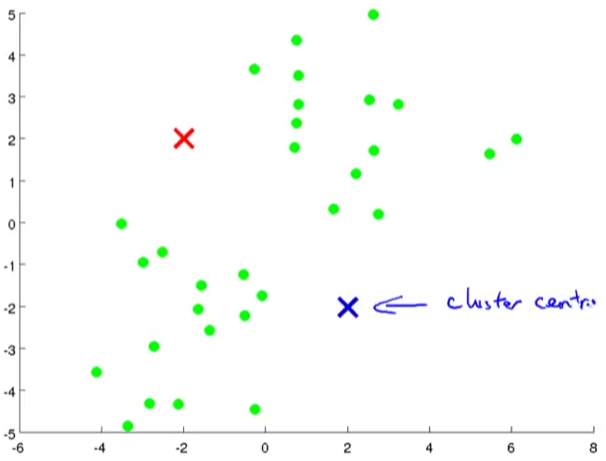
2.然后计算所有点和两个点的距离,离哪个聚类中心点近就把他归为同一类:
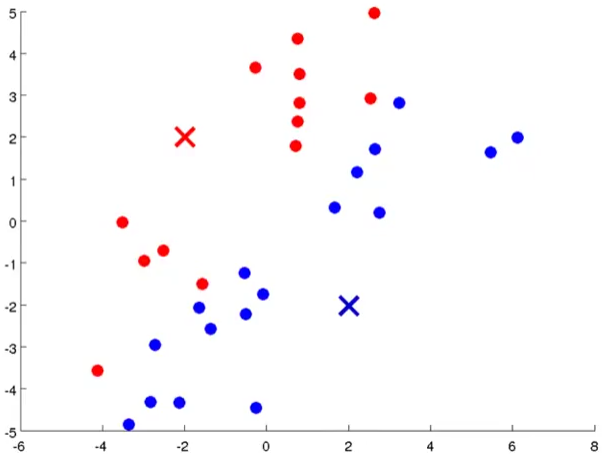
3.然后将聚类中心点移动到同一类点的均值处,也就是位置中心:
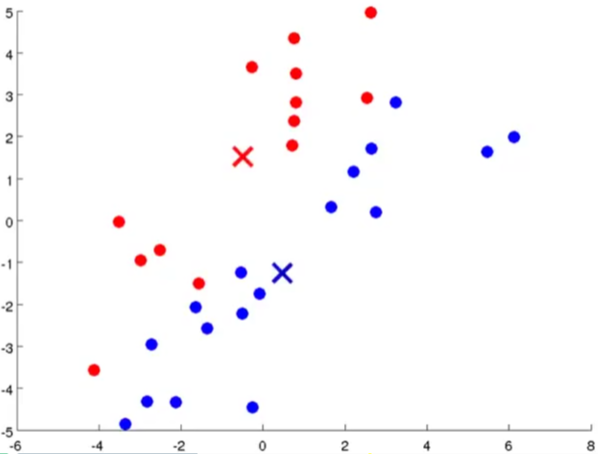
这就是移动之后的图,有人会问为什么会这样移动,因为对于蓝色的点,下面相对集中,所以移动之后相对原来会偏下一点,而红色的点上面的多一点,所以移动之后会比原来偏上一点。
4.然后重复上面两个步骤。
原理的抽象化
聚类算法有两个输入:
- 要分类的数量K
- 训练数据
运作流程:
- 先随机生成K个聚类中心,每一个聚类中心代表一类数据
- 然后重复以下流程
- 对所有的点计算相对每一个聚类中心的距离,并把这个点归类为距离最近的那个聚类中心点那一类。
- 计算所有同一类的点的均值,然后将该类的聚类中心移动到均值处。
这样循环到最后,所有的聚类中心点最后会停在某一个地方,算法也就收敛了。
优化目标
之前的有监督学习,都是有一个优化目标的,而无监督学习实际上也是有的。
首先定义这样几个表示法:

首先是C<sup>(i)</sup>表示第i个样本为第几类。μ<sub>k</sub>表示第k个聚类中心点。μ<sub>c<sup>(i)</sup></sub>表示第i个样本的聚类中心点。
所以优化目标为:
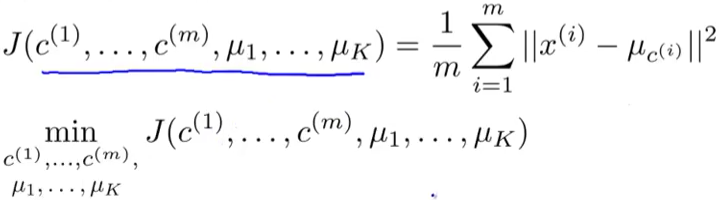
这个代价函数在K-Means里面也叫做是真代价函数。实际上从数学上可以证明,我们上面的做法就是最小化了这个目标函数。
Tips: wrt表示with respectd to
看这个还顺带学了点英语XD
避免局部最优
有很多方法可以用来帮助我们在算法中,避免局部最优解,那就从随机初始化开始吧。
随机初始化
随机初始化也有很多方法,常见的一种是随机选几个样本点作为聚类中心点。以二分类为例如下:
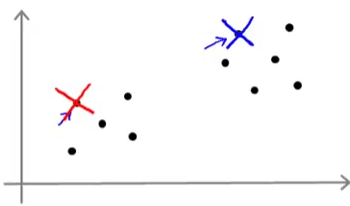
光是一次随机初始化还不够,有时候也会陷入局部最优解,所以要多次随机初始化,每一次随机初始化对应了一个结果,然后在多个结果里面找一个最优的解。
如何选择分类数K
说是教你如何选,但其实也只是模棱两可的。。。。的。。。。。????
但是有一个猪肘法则,不是,是肘部法则,可以帮你来选择到底分成几类。
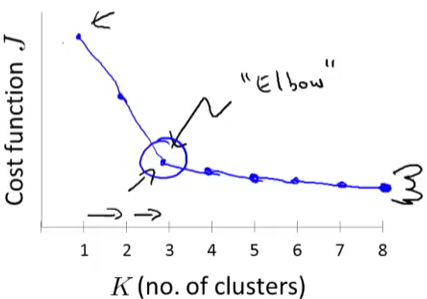
如果你得到了一条类似于这样的曲线,那么很好,分成三类会是一个合理的选择。
但现实是骨感的,总是残酷的,你大多数时候只能得到这样的曲线:
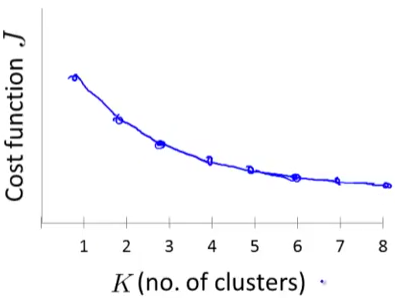
并没有一个很明显的猪肘,那么就只能在心里#%^@&!^@@&!^@…..此处省略一万字。
更一般的说,我们用分类算法,肯定有一个下游目的,那么看分成多少类更有利于我们之后的目的,才是正解。(相当于没说)
维数约减(Dimensionality Reduction)
刚刚听到的时候,不明觉厉。
维数约减是另一类无监督学习问题,使用这个的原因之一是,我们希望数据压缩(Data Compression),数据压缩不仅仅可以使得占用内存减小,而且可以帮助算法提速。
数据压缩
数据压缩就是,将高维的数据映射到低维,然后用更小维度的数据来表示高维数据。
数据可视化
将高维数据,映射到两维去,这样就可以观察各个数据之间的关系,尽管这样里面还是会牺牲很多细节在里面,而且被映射的二位数据通常没有什么物理意义。
主成分分析法(Principal Componet Analysis, PCA)
如果说上面那些都是概念,那么主成分分析法就是如何实现上面那些概念。
PCA能吃吗
主成分分析法做的一件事情就是,以二维数据为例,要找一条线来将所有的数据投射到上面去:
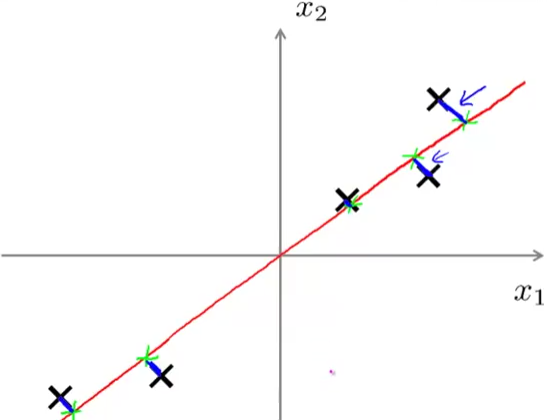
而每个点到直线的距离,也就是图中的蓝线,就叫做投射误差,PAC做的事情就是尽量减小这个投射误差。
Tips:说到这里,我就迷糊了一下,感觉PCA和回归有点像,但又说不出来差别。
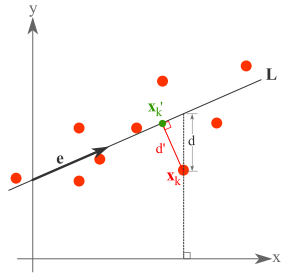
差别就在这里:
- PCA使用上图的d’来衡量投影的好坏,使得样本到直线的距离最小。
- 线性回归使用上图中的d来衡量回归的好坏,使得f(x)-y的平方和最小。
- 顺带一说,最小二乘法(最小平方法),使得f(x)-y的平方值最小化,线性回归使用的是最小二乘法。
如何实现PCA
说了那么多有的没的,到底如何才能实现PCA呢?
- 老规矩,首先对数据进行预处理,包括缩放等等。
- 求协方差
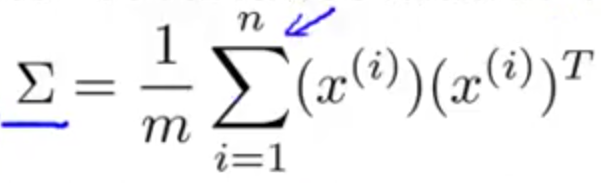
- 计算这个协方差矩阵的特征向量
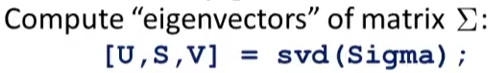 其中返回值
其中返回值U就是你需要的,特征值矩阵。 - 取出
U的前k列元素Ureduce,然后z=Ureduce'*x。
如何还原被压缩的数据
有一点计算机知识的人都知道,数据压缩之后,通常来说都会有一点失真,所以对于PCA而言,也是一样,想要完全恢复是不可能的,但是恢复的差不多却是可以的。
想要还原数据,只需要将上面的乘式反过来即可:

这个过程也叫做原始数据的重构(Reconstruction)。
如何选择K
又到了一年一度的参数选择环节,今年又带来怎么样的选择方案呢?
一般来说,会选择平均平方映射误差小于0.01的K值:
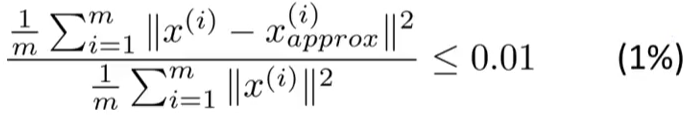
这个也表示,有99%的数据差异性被保留。另一个常用的数值是0.05。
那么求一个K值得过程可以分为三步:
- 取K=1
- 计算压缩后的数据
- 计算上面的平均平方映射误差,如果满足条件,结束;不满足条件,就将K加1,然后重复此过程。
你会发现,第三步计算平均平方映射误差会很耗费时间,因为计算量大。但是有一个东西可以帮助我们更简单的计算这个值。
在之前求特征向量的计算中,你也可以得到特征值矩阵:
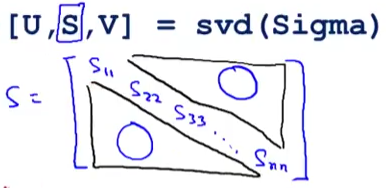
这个S就是特征值矩阵,一个对角阵,然后下面这个式子就可以轻松地求出平均平方映射误差:
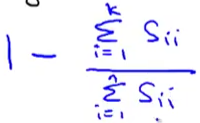
上式右边分子是前K个对角元素之和,分母是对角所有元素之和。
这样,你就不用计算被压缩后的数据,也不用计算被压缩后的数据和原数据之间的平均平方映射误差,只需要增加K,然后计算上式就好了。
总结一下就是(实在懒得手打XD):

Tips
将这个应用于你的各种算法来说,请只将训练集进行PCA数据压缩就好,而将得到的原数据映射到压缩数据的规律应用到交叉验证集或者测试集,而不是将PCA应用于这些。
也不要把PCA用来解决过拟合,解决过拟合的好方法是添加正则化。尽管用PCA之后看起来降低了过拟合,但实际上并不是真正的解决了过拟合。
不要在设计算法之初,就将PCA囊括进来,先使用原始数据来看看效果才是应该有的顺序,而后发现真的需要压缩数据,提升速度,在有充足的理由使用PCA的时候,才去使用PCA。
后记
啊啊啊啊啊,这一周又完结了,撒花!!!!刚刚边学的时候,就有人留言问我博客的问题,然后我发现,还有好多坑等着我去填呢